تانسورها در سراسر ریاضی و علوم برای آشکار کردن حقایق هندسی پنهان استفاده میشوند. آنها چه هستند.
پس از آنکه آلبرت انیشتین نظریه نسبیت خاص خود را در سال ۱۹۰۵ منتشر کرد، دهه بعدی را صرف تلاش برای ارائه نظریهای برای گرانش کرد. اما سالها، او مدام با یک مشکل روبرو میشد.

او میخواست نشان دهد که گرانش در واقع نوعی تاب برداشتن هندسه فضا-زمان است که در اثر وجود ماده ایجاد میشود. اما او همچنین میدانست که زمان و مسافت به طور غیر شهودی نسبی هستند: آنها بسته به چارچوب مرجع شما تغییر میکنند. حرکت سریع باعث میشود فواصل کوتاه شوند و زمان کند شود. پس چگونه میتوانید گرانش را به طور عینی توصیف کنید، صرف نظر از اینکه ساکن هستید یا در حال حرکت؟
انیشتین راه حل را در یک نظریه هندسی جدید که چند سال قبل توسط ریاضیدانان ایتالیایی، گرگوریو ریچی-کورباسترو و تولیو لوی-چیویتا، منتشر شده بود، یافت. در این نظریه، پایه ریاضی چیزی نهفته بود که بعدها «تانسور» نامیده شد.
از آن زمان، تانسورها نه تنها در نظریه نسبیت عام انیشتین، بلکه در یادگیری ماشین، مکانیک کوانتومی و حتی زیستشناسی نیز نقش مهمی داشتهاند. دیونیسیوس آنینوس گفت: «تانسورها کارآمدترین دستگاه بستهبندی هستند که ما برای سازماندهی معادلات خود داریم.»(یک برگه جدید باز میکند)، یک فیزیکدان نظری در کالج کینگ لندن. «آنها زبان طبیعی برای اشیاء هندسی هستند.»
تعریف آنها نیز دشوار است. با یک دانشمند کامپیوتر صحبت کنید، ممکن است به شما بگوید که یک تانسور آرایهای از اعداد است که دادههای مهم را ذخیره میکند. یک عدد، تانسور «رتبه ۰» است. لیستی از اعداد، که بردار نامیده میشود، تانسور رتبه ۱ است. یک شبکه از اعداد یا ماتریس، تانسور رتبه ۲ است. و غیره.
اما اگر با یک فیزیکدان یا ریاضیدان صحبت کنید، متوجه میشوند که این تعریف ناقص است. از نظر آنها، اگرچه تانسورها را میتوان با چنین آرایههایی از اعداد نمایش داد، اما معنای هندسی عمیقتری دارند.
برای درک مفهوم هندسی تانسور، با بردارها شروع کنید. میتوانید یک بردار را به عنوان یک پیکان شناور در فضا در نظر بگیرید – این پیکان دارای طول و جهت است. (این پیکان نیازی به اتصال به یک نقطه خاص ندارد: اگر آن را در فضا حرکت دهید، همان بردار باقی میماند.) یک بردار میتواند سرعت یک ذره را نشان دهد، به عنوان مثال، طول آن نشاندهنده سرعت و جهت آن است.
این اطلاعات در فهرستی از اعداد بستهبندی میشوند. برای مثال، یک بردار در فضای دوبعدی توسط یک جفت عدد تعریف میشود. عدد اول به شما میگوید که فلش چند واحد به سمت راست یا چپ امتداد یافته است، و عدد دوم به شما میگوید که چقدر به سمت بالا یا پایین امتداد یافته است.
اما این اعداد به نحوه تعریف سیستم مختصات شما بستگی دارند. فرض کنید سیستم مختصات خود را تغییر میدهید:
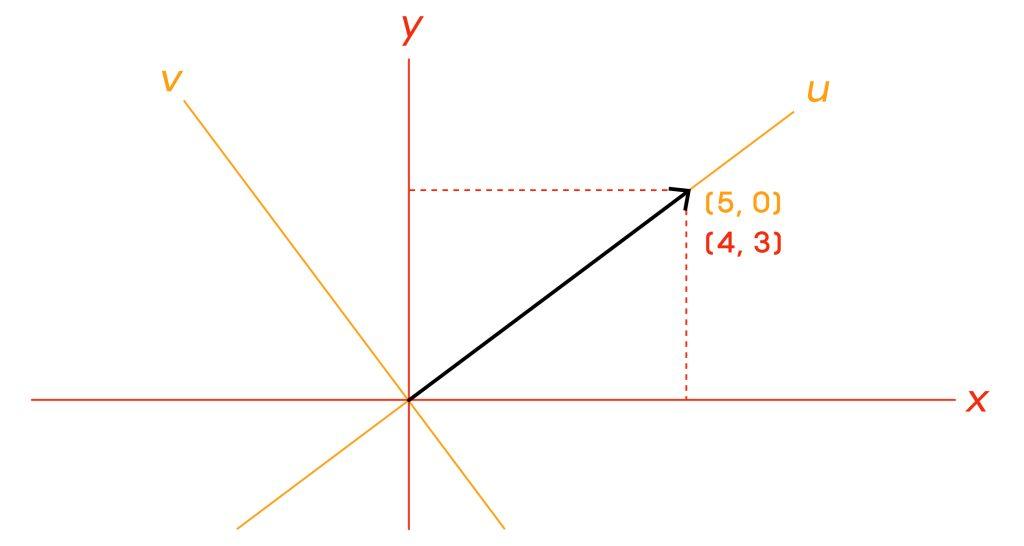
هکنون بردار را بر اساس میزان امتداد آن در هر جهت از سیستم مختصات جدید بیان میکنید. این به شما یک جفت عدد متفاوت میدهد. اما خود بردار تغییر نکرده است: طول و جهت آن، صرف نظر از سیستم مختصاتی که در آن هستید، ثابت میماند. علاوه بر این، اگر بدانید چگونه از یک سیستم مختصات به سیستم مختصات دیگر بروید، به طور خودکار خواهید دانست که لیست اعداد شما چگونه باید تغییر کند.
تانسورها این ایدهها را تعمیم میدهند. یک بردار، تانسوری با رتبه ۱ است؛ تانسورهای با رتبه بالاتر حاوی اطلاعات هندسی پیچیدهتری هستند.
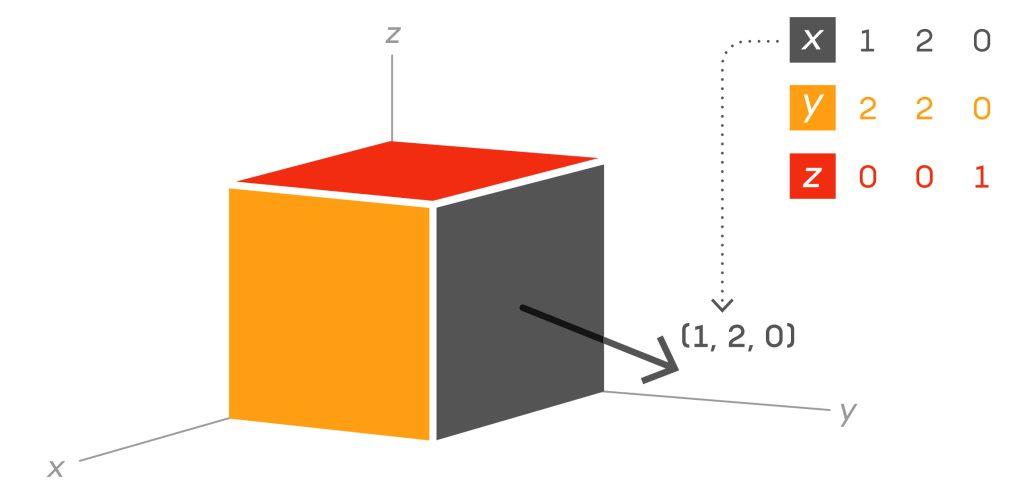
برای مثال، تصور کنید که یک بلوک فولادی دارید و میخواهید تمام نیروهایی را که میتوانند بر آن وارد شوند توصیف کنید. یک تانسور مرتبه ۲ – که به صورت ماتریس نوشته میشود – میتواند این کار را انجام دهد. هر یک از وجوه بلوک، نیروها را در سه جهت مختلف احساس میکند. (برای مثال، وجه راست بلوک میتواند نیروها را در جهت بالا-پایین، جهت چپ-راست و جهت جلو-عقب تجربه کند.)
ریاضیدانان اغلب تانسورها را به عنوان توابعی تصور میکنند که یک یا چند بردار را به عنوان ورودی میگیرند و یک بردار دیگر یا یک عدد را به عنوان خروجی تولید میکنند. این خروجی به انتخاب سیستم مختصات بستگی ندارد. (این محدودیت همان چیزی است که تانسورها را به طور کلی از توابع متمایز میکند.) به عنوان مثال، یک تانسور ممکن است دو بردار را که لبههای یک مستطیل را تشکیل میدهند، دریافت کند و مساحت مستطیل را به عنوان خروجی ارائه دهد. اگر مستطیل را بچرخانید، طول آن در امتداد محور
x و ارتفاع آن در امتداد محور y تغییر خواهد کرد. اما مساحت آن تغییر نخواهد کرد.

از زمان انتشار این معادله در سال ۱۹۱۵، تانسورها فراگیر شدهاند. فیزیکدانان از آنها برای توصیف حرکت الکترونها در اطراف هستههای اتمی یا توصیف وضعیت یک سیستم کوانتومی درهمتنیده استفاده میکنند. دانشمندان کامپیوتر از آنها برای ذخیره پارامترهای مدلهای یادگیری ماشین استفاده میکنند. زیستشناسان از آنها برای ردیابی صفات در طول یک نسل استفاده میکنند. و ریاضیدانان آنها را در هم ضرب میکنند تا تانسورهای پیچیدهتری بسازند و سپس فضاهای جدیدی را که تانسورها در آنها قرار دارند مطالعه کنند. تانسورها میتوانند به ریاضیدانان کمک کنند تا تقارنهای پیچیده را کشف کنند، خواص اشکال خاصی به نام منیفولد را تجزیه و تحلیل کنند و روابط بین توابع مختلف را بررسی کنند.
انیشتین زمانی از یکی از دوستانش التماس کرد که در درک تانسورها به او کمک کند، زیرا میترسید دیوانه شود. اما او آنها را درک کرد -و از آن زمان تاکنون، تانسورها کلید توانایی دانشمندان برای توصیف جهان ما بودهاند.